7 Ways To Do Sequential Numbering in Microsoft Access

Occasionally we come across project requirements that include the ability to do sequential numbering in Access on a set of data. We cannot just use the auto-number data type because there is no promise of sequentiality but only uniqueness. In other words, if someone creates a record then later deletes it, there will be a gap in the sequence. So, what are our options? There are actually several ways, each with its pros and cons.

1. Let SQL Server Do It

If you have a SQL Server backend, you could just use the windows function ROW_NUMBER() and define it as a part of a SQL Server view. This is probably the simplest, no-nonsense method that works well for any purposes. This was introduced in SQL Server 2005 so chances are high you can use it if you can create views.

Swell, but I don’t have a SQL Server backend.

In fact, we have had run into cases like this and we can still do it without the ROW_NUMBER() function. Let’s look at few sequential numbering methods that can be done entirely in Access…

2. Use a Report with Running Sum Property

If your objective is to generate a report, then you don’t want numbering to be a part of your query but rather a part of the report itself. You can use the “Running Sum” property of a textbox on a report to do all the work for you:

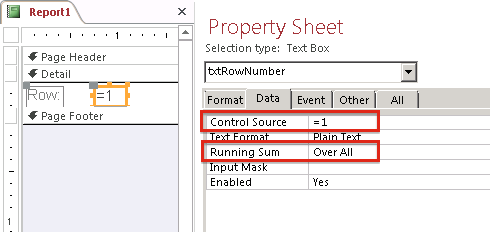
3. …But I’m Exporting Raw Query Data

The Running Sum method works great as long you are happy with creating and running an Access report, but not all requirements want the data in an Access report. Sometimes we do need to export a content of query and therefore we can’t use a report (or at least we don’t want extraneous formatting contents when we try to export a report).

To do this entirely in a query, we need a bit of help from the VBA. We need to create a brand new VBA standard module and define a module-level variable, and two functions:
Private lngRowNumber As Long

Public Function ResetRowNumber() As Boolean
lngRowNumber = 0
ResetRowNumber = True
End Function

Public Function RowNumber(UniqueKeyVariant As Variant) As Long
lngRowNumber = lngRowNumber + 1
RowNumber = lngRowNumber
End Function
Then within your query’s SQL, you should call the functions as so:
SELECT RowNumber(TablePrimaryKey) As RowNum
FROM SomeTable
WHERE ResetRowNumber()
ORDER BY SomeColumn;
Let’s look at why we have this setup. It seems strange to put a ResetRowNumber() call in a WHERE clause, doesn’t it? However, the WHERE clause is actually resolved prior to the SELECT clause. (For those who wants to geek out on SQL internals, Itzik Ben-Gan, a SQL Server MVP has a great post that outlines the logical query processing. Though this is specific to SQL Server, the Access database engine as well the majority of RBMS engines generally follow the same outline). This gives us a convenient point to ensure that the module level variable lngRowNumber is always correctly reset at the right time (e.g. before we start returning records from a query).

Now, what’s the deal with the UniqueKeyVariant parameter for the RowNumber() function? We are not even using it all! True, but if we didn’t, Access will call RowNumber() only once for an entire query and thus we get “1” for the entire dataset. That is a good way to save on CPU processing – why call Now() for each row? In this case, we want to go against this CPU-saving measure and ensure that the RowNumber() is in fact called once per row to generate a new number for that row. Thus, we pass in a parameter — a primary key of a table is a good choice for this purpose. So we get a nice sequential number generated all in the query with VBA function.

Finally, though it won’t be required, having a ORDER BY clause is probably going to be very essential. Without an explicit sort applied to query, you might find that sequential numbers are sequential… but to the wrong rows! It’s entirely up to you to define how it should be sorted so the sequential numbers make sense.

4. Hey, I Opened This in a Datasheet and It’s All Messed Up!

Ah, that’s the con – this works beautifully when you are in fact exporting data but when you are viewing the query’s output in a datasheet or a form, as you scroll around, Access will be re-evaluating the rows, including a call to the RowNumber(). But when it repeatedly calls RowNumber(), of course it keeps incrementing blindly, without any regards to whether a number was already generated for that row.

So, if you wanted to use this idea in a form or datasheet, let me stop and first remind you – if this is going to be non-updatable, you can just embed a report as a subreport within a form and thus use Running Sum. But let’s discuss the case where you need to be able to edit data in the forms, even with sequential numbering generated for the data you are viewing. This means we need to be able to tie a sequential number to a specific row.

The best way to do this is to use a primary key. In cases where a query is complex and joins several tables, we may need to use the primary key of the table that’s on the bottom of the relationship hierarchy or possible a concatenation of multiple tables’ unique key so that the expression will be unique and thus we can identify which sequential number we have assigned.

We will then modify the mdlRowNumbers module accordingly:
Private lngRowNumber As Long
Private colPrimaryKeys As VBA.Collection

Public Function ResetRowNumber() As Boolean
Set colPrimaryKeys = New VBA.Collection
lngRowNumber = 0
ResetRowNumber = True
End Function

Public Function RowNumber(UniqueKeyVariant As Variant) As Long
Dim lngTemp As Long

On Error Resume Next
lngTemp = colPrimaryKeys(CStr(UniqueKeyVariant))
If Err.Number Then
lngRowNumber = lngRowNumber + 1
colPrimaryKeys.Add lngRowNumber, CStr(UniqueKeyVariant)
lngTemp = lngRowNumber
End If

RowNumber = lngTemp
End Function
Basically, the only difference is that we now maintain a VBA.Collection, and this time we do make use of the UniqueKeyVariant parameter, using it as a key to locate the previously assigned number. If we don’t find it, we add to the VBA.Collection. The SQL to use those 2 functions remains identical. The downside is that if the query generates millions worth of rows, the memory may run out due to a large VBA.Collection. However, if a form is bound to that large dataset, it will likely have several other problems anyway so VBA.Collection should not be a problem for forms that loads a few hundred rows. The other downside is that VBA.Collection will persist indefinitely even long after the query has “finished.” Back to form example, you might need to remember to call the ResetRowNumber() function on a form’s close to ensure that you dispose of the VBA.Collection and free up the memory.

5. But I Need it for Multiple Forms; I Can’t Have Several VBA.Collection Instances!

The problem with the previous example is that it’s OK since you only need it in one place but if you will have several places where it is used, you now have to qualify the instance of VBA.Collection to each place – not insurmountable but too easy to get messy and hairy very fast.

However, there is a property we can use to get ourselves out of this problem and that is the AbsolutePosition property of the recordset. We can create a textbox, bind it to expression “=RowNumber()” and then create a function on the module behind the form that references the recordset:
Public Function RowNumber() As Variant
On Error Resume Next
If Me.NewRecord Then
If Me.Dirty Then
RowNumber = Null
Exit Function
End If
End If

With Me.RecordsetClone
.Bookmark = Me.Bookmark
RowNumber = .AbsolutePosition + 1
End With

If Err.Number Then
RowNumber = Null
End If
End Function
This requires no pre-knowledge of a primary key and only assumes that when you load the form initially, it is already sorted. Any records newly inserted will get the next bigger number. However, if you requery and it causes the newly inserted rows to be re-sorted, they will be now given a new number that relates to their actual position within the set, which can be either good or bad, depending on your specific requirements.

You might find it useful to ensure that the RowNumber() is called after insert of records, perhaps with this code:
Private Sub Form_AfterInsert()
'Assumes there's a textbox named txtRowNumber
'and it is bound to expression "=RowNumber()"
Me.txtRowNumber.Requery
End Sub
You also will find the code much easier to re-use, perhaps by packaging into a class module and thus encapsulate the implementation while sharing among several forms without worrying about VBA.Collections bloating since you are just using an innate property of the Recordset object.

6. Use the Auto-Number, Luke

Yet another approach that does not require embedding VBA functions into your SQL is to just create a new table and insert data into it. That requires at least three SQL statements to do this:
DROP TABLE tmpSomeTempTable;

CREATE TABLE tmpSomeTempTable (
RowID AUTOINCREMENT,
SomeColumn TEXT(255)
);

INSERT INTO tmpSomeTempTable (
SomeColumn
)
SELECT
SomeColumn
FROM tblSomeTable
ORDER BY SomeColumn;
Note this works only because we create a brand new table, add an autonumber column to it as well any other columns we need then insert records into it. It’ll be contiguous – as long we don’t delete any records from the table. Unfortunately, creating a brand new table every time we run this will result in bloat of the Access file – if you can do it in a separate Access file, all the better so that you can compact it when you need to.

This also either requires 3 separate saved queries or 3 separate calls to DAO.Database.Execute methods, for each SQL statement, in addition to handling the error when the temporary table doesn’t exist. The simplest and clean method for this case could be this following VBA code:
Dim db As DAO.Database
Set db = CurrentDb()

db.Execute strDropTableSQL ‘Do not use dbFailOnError parameter
db.Execute strCreateTableSQL, dbFailOnError
db.Execute strInsertDataSQL, dbFailOnError
By omitting the dbFailOnError parameter only for the DROP TABLE statement, we won’t get a runtime error about a table not existing but get runtime errors if we can’t create the table or insert data for some reasons. I’m also not a big fan of creating multiple saved queries that are meant to be logically grouped together – it gets quite cluttered when there are several saved queries in a navigation pane like that. Keeping it all in VBA makes it clearer that the intention is to execute those statements together.

7. Why Not Do it all in a Single SQL Statement? I Saw a Method that Does This…

Yes, it is certainly possible to do it without VBA at all. One possible method is to write a subquery that counts all rows up to this row. This also assumes there is a primary key that you can use and you can define a sort order. Here’s a sample SQL:
SELECT
(
SELECT COUNT(*)
FROM SomeTable AS x
WHERE x.PrimaryKey <= t.PrimaryKey
ORDER BY x.SomeColumn
) AS RowNumber
FROM SomeTable AS t
ORDER BY t.SomeColumn;
This will work OK for a small set of data, but the more data there is, the more intensive the subquery becomes, and it must be called repeatedly for each row. This is one of those rare cases where doing it in VBA is faster than doing it in SQL — after all, row numbering is fundamentally iterative, not set-based which just goes against the grain of what SQL was designed to do – solve a problem in a set-based fashion, non-iterative fashion.

There are also other problems – for one thing, it’s not a very generic solution. You must customize several parts to work for different queries. If the set of tables used in the outermost FROM clause are different, to be the innermost FROM clause, you have to adjust the WHERE clause to reference the correct primary key (or some combination thereof). Then you have to also keep the ORDER BY in sync. That’s a lot of tweaks if you want to use it for different queries. That is why this is the last method listed here but it is one possible solution.

So Many Ways to Number a Cat

As you can see, an idea of sequential numbering can be solved many different ways using different domains. This is typical in this field of work and precisely why it pays to not just consider how you can do it in one domain but also whether the domain is the right domain. We saw how we can easily leverage built-in features such as Transact-SQL’s ROW_NUMBER() or Access report’s Running Sum property. We also not only saw how we can craft our custom solutions in either VBA or SQL but we also see how we can use both together to create a solution that is better.

So in the end, it is good to look at the final goal first rather than the intermediate steps and think about the domains that might be better suited to get you there.